Why we moved to 256-bit AES keys

What are 256-bit AES keys?

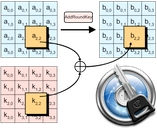
AES (the Advanced Encryption Standard) is a fundamental building block of the encryption within 1Password and most everything else that uses encryption in the modern world. It takes a key and some data (plaintext) as input and transforms that data into something that looks entirely random (ciphertext). The only way to get meaning out of the ciphertext is to use AES and the same key to transform it back into the plaintext. A key is just a number, and AES can work with keys of three different sizes, 128 bits, 192 bits, and 256 bits.

AES, by the way, is always a 128-bit cipher operating on 128-bit chunks of data (blocks) at a time; so when I use expressions like “AES256” or “256-bit AES” in what follows, I’m just talking about key size.

Talking about big numbers

The numbers that we need to talk about are just too big to write out normally. When we are dealing with numbers like 65536, I can opt whether to express it as “65536” or “2 to the power of 16”, depending on what is most useful in the context. And maybe when dealing with a number like “2 to the power of 32” I can say things like “4.3 billion”.

“2 to the power of 128” in words

“three hundred forty undecillion, two hundred eighty-two decillion, three hundred sixty-six nonillion, nine hundred twenty octillion, nine hundred thirty-eight septillion, four hundred sixty-three sextillion, four hundred sixty-three quintillion, three hundred seventy-four quadrillion, six hundred seven trillion, four hundred thirty-one billion, seven hundred sixty-eight million, two hundred eleven thousand, four hundred fifty-six”

But the numbers we deal with in cryptography are so big that I have to write them in exponential form. The number of possible keys that a 128-bit key allows is just too enormous to write otherwise. Sure, I could write out “2 to the power of 128” in words with the help of a numbers to words converter, but it is neither informative nor manageable. Nor would it be useful for me to write out the number in decimal, as it would be 39 digits long.

And one more thing about writing numbers in words: when I do so here, I will be using the US English, short scale, conventions; “billion” means “10 to the power of 9”, not “10 to the power of 12”.

Searching for keys is harder than digging up bones

Molly (one of my dogs) doesn’t really enjoy dog toys that much, but she will certainly not allow Patty (the other dog) to play with any toys. Molly, then, steals and hide Patty’s toys. Suppose that Molly has a possible “2 to the power of 128” sniff-proof hiding places she can hide them in. Also suppose that Patty knows about all of those hiding places, but she doesn’t know which one Molly has used. Patty might try to look in each one until she finds her toys. Searching each and every one of those “2 to the power of 128” hiding places until she finds the one with the toy is what we’ll call a brute force attack.

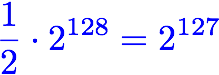
On average, Patty will find the right one after searching about half way through all of the hiding places. This means that, on average, she’ll have to try “2 to the power of 127” hiding places before she finds her toys. If you thought it was going to be “2 to the power of 64”, pause for a moment. In fact, “2 to the power of 128” divided by 2 is “2 to the power of 127”. Each additional power of two doubles the number, so halving the number means just taking one off of the exponent.

Molly might imagine that, to be extra secure instead of using ‘only’ “2 to the power of 128” possible hiding places, she might use “2 to the power of 256” possible hiding places. “2 to the power of 256” is enormously bigger than “2 to the power of 128”. Hugely bigger. Unimaginably bigger. Mind-boggingly bigger, though to be honest, the number 2 is enough to boggle Molly’s mind. In fact, “2 to the power of 256” is “2 to the power of 128” times bigger than “2 to the power of 128”.

Now, I just said that moving to “2 to the power of 256” hiding spaces makes the number of places that Patty would need to search unbelievably, enormously, mind-bogglingly bigger. But Molly would be wrong to think that this made it more secure. Why? Because searching through ‘only’ “2 to the power of 128” hiding spaces is already so mind-bogglingly, amazingly and unimaginably hard that there is no gain in making it harder.

How long is long?

Patty is a very fast dog – well, at least in her youth she was. Even today, over short distances, she can outrun Molly, who is ten years her junior. So let’s imagine that Patty could search hiding spaces as quickly as a super computer can add two numbers. Actually, let’s suppose that she gets together with a billion other dogs, each of which can search a hiding place as quickly as it takes a super computer to add two numbers. Working at this unimaginable speed, these billion super fast dogs working under Patty’s direction might be able to search “2 to the power of 50” hiding spaces per second, which is about one quadrillion hiding spaces per second. There are about 31557600 seconds per year, so working like a billion super computers, Patty with her friends could check about “2 to the power of 75”, or 10 septillion, hiding places per year.

At that rate it would take “2 to the power of 53” years (10 quadrillion years) to work through half of the “2 to the power of 128” hiding spaces. If we take the universe to be about 15 billion years old, then the amount of time it would take Patty, working faster than the combined power of a billion super computers, would be more than 600,000 times the age of the universe.

In case my analogy has gone too far astray, I’m estimating that, as an extremely fast estimate, all of the computing power on Earth turned to trying AES keys couldn’t check more than “2 to the power of 75” keys per year (and really that is a very very high estimate). At that rate, it would take more than half a million times the age of the universe to go through half of the “2 to the power of 128” possible AES keys.

Now, single-minded Molly, who will spend an entire day barking at a squirrel up a tree, may think that half a million universes ages isn’t too long to wait. But nobody else would even consider trying such a brute force attack. Patty is a clever dog, and so she wouldn’t even consider trying a brute force attack on “2 to the power of 128” hiding spaces.

Patty might try other attacks. She might figure that Molly didn’t pick the hiding place in a truly random fashion, and so Patty might know which sorts of places to search first. Or Patty might try to secretly follow Molly to the hiding place. Or maybe there is a way that Patty can trick Molly into bringing her the toys. Those are the kinds of attacks that Molly needs to defend against. But she gains nothing by increasing the number of possible hiding places, because even if Patty had all of the resources on Earth searching Molly’s hiding places, Patty couldn’t even make a dent before the universe comes to an end.

The difference between zero and zero is zero

The chances of Patty and all of her super fast friends finding Molly’s hiding spot is as close to zero as we could possibly want. Let’s call Patty’s chances in this case “epsilon 1”, a really small number. If Molly uses “2 to the power of 256” possible hiding spaces instead of “2 to the power of 128”, the chances of Patty and her friends finding the one with the toys is another number as close to zero as we could possible want. We’ll call these chances “epsilon 2”. Sure, “epsilon 2” is many times smaller than “epsilon 1”, but both “epsilon 1” and “epsilon 2” are already as close to zero as we could possibly want. Molly’s practical security gain in using the larger number of hiding spaces is pretty much the difference between “epsilon 1” and “epsilon 2”. That difference, for all meaningful purposes, is zero.

It takes a lot of dog food to keep Patty searching

We all know that dogs like to eat. And we all know that computers consume electricity. As it happens, computation (and inspecting hiding places) has to consume energy. It’s actually the destruction (or overwriting) of information that necessarily consumes energy, but that happens when Patty forgets about a previous hiding place so she can think about the next one. If Patty and her friends could move on to checking a new possible key using the absolute theoretical minimum energy for a single computation, 2.85 × “10 to the power of -21” J, she and her pack of billion super fast (and now unfathomablely efficient) of dogs would require about 1/100th of the total amount of energy humanity uses in a year to work through half of the “2 to the power of 128” hiding spaces.

The answers to some questions remain TOP SECRET

I have tried to explain all this to Molly countless times, but she just stares blankly as if to ask, “Well, then why does the US government require 256-bit AES keys for TOP SECRET material?” Actually, all Molly says with her stares is, “Huh?”. I tend to read a bit more into these than is really there. My only answer to her is that it is the same reason that she likes being blow dried after a bath on her left side, but hates it on her right side. Some things, in the mind of Molly and in government, remain a mystery.

I have some reasonably charitable speculation for why those requirements are there, but it remains speculation, and we can continue that discussion in our discussion forums.

Are 256-bit keys less secure than 128-bit keys?

When Bruce Schneier advises:

[F]or new applications I suggest that people don’t use AES-256. AES-128 provides more than enough security margin for the [foreseeable] future. But if you’re already using AES-256, there’s no reason to change.

People need to pay attention. But paying attention and evaluating doesn’t always mean agreeing.

Briefly, there is a long-known problem with how AES deals with 256-bit AES keys. (Of course in this business a “long-known problem” means about 10 years old.) AES does multiple rounds of transforming each chunk of data, and it uses different portions of the key in these different rounds. The specification for which portions of the key get used when is called the “key schedule”. The key schedule for 256-bit keys is not as well designed as the key schedule for 128-bit keys. And in recent years there has been substantial progress in turning those design problems into potential attacks on AES 256. This is the basis for Bruce Schneier’s advice on key choice.

One of the two reasons why I reject Schneier’s advice is that the issue with the AES 256-bit key schedule only opens up the possibility of a related key attack. Related key attacks depend on things being encrypted with keys that are related to each other in specific ways. Imagine if a system encrypts some stuff with a key, k1 and encrypts some other stuff with a different key, k2. The attacker doesn’t know what either k1 or k2 are, but she does know the difference between those two keys are. If knowing the relationship between keys (without knowing the keys) gives the attacker some advantage in discovering the keys or decrypting material encrypted with those keys, then we have a related key attack.

When cryptographic systems are properly designed, related key attacks should not be relevant because good crypto systems shouldn’t use or create related keys. Cryptographers worry about related key attacks on AES because they know that some systems will be poorly designed, so it is still important to build ciphers that aren’t vulnerable to related key attacks. A spectacular case of using related keys with a cipher (RC4) for which related key attacks were easy was probably the design WEP WiFi encryption standard. This is one of several reasons why it is possible to discover a WEP Wi-Fi key after just a few minutes (though remember: Just because it’s easy doesn’t mean it is right or legal).

Each and every encryption key used in 1Password is selected independently using a cryptographically appropriate random number generator. This means that there is no way for an attacker to know of any relationship among keys used or generated by 1Password. There is no relationship among keys.

So why 256 bits?

I hope I’ve persuaded you that 256-bit AES does not reduce any meaningful threat. Essentially it reduces the chance of a successful brute force attack from effectively zero to effectively zero.

So why the move to 256-bit AES keys?

1Password data needed to be encrypted and decrypted on first generation iPhones. Lots of encryption operations using 256-bit keys would have been slow and would drained batteries faster. On desktop computers, we were able to move to 256-bit keys within our 1Password browser extension. But for our principal data format – the one that is used across platforms – we needed to consider the minimal hardware it would run on.

1Password 4 for iOS requires iOS version 6 (which includes development features that allows for our awesome new Web Mode). This means all the devices 1Password 4 will run on are sufficiently powerful that we no longer need to be concerned about performance issues with 256-bit keys. The performance concerns that we had in the past—both speed and power consumption—are no longer a concern today.

2. Tougher key derivation

This one is subtle. And I’d like to thank Solar Designer of the Openwall Project for drawing my attention to this. It turns out that a side effect of using 256-bit keys in 1Password can make things even harder for automated Master Password guessing programs, not because such keys are harder to attack, but through a more convoluted chain. Don’t worry if you find this section confusing.

1Password uses PBKDF2 to slow down password crackers that could be used to automate guessing your Master Password if someone gets hold of your data. PBKDF2 is a Key Derivation Function – a system that churns your Master Password into a number that can be used as an encryption key. With our new Cloud Keychain Format, we use PBKDF2 to turn your Master Password into two 256-bit keys. One is an HMAC key, used for an integrity check on the data; and the other is a key used to actually decrypt the master key. To derive that total of 512-bits from your Master Password, 1Password uses HMAC-SHA512 within PBKDF2 in the Cloud Keychain format.

Password cracking systems, like hashcat, can speed up their operations by using GPUs (Graphic Processing Units) which can perform some kinds of computations blindingly fast, but there are some computation artifacts of SHA-512 that make this harder on GPUs. Solar Designer mentions this in his discussion of the future of password hashing (slide 35 and elsewhere).

I did warn you at the beginning of this section that this particular reason is convoluted and subtle. The short version is that a side-effect of using 256-bit AES keys is that it makes PBKDF2 more effective in certain circumstances.

3. People (and Molly) feel better about 256-bit keys

If Molly feels that 128-bit keys aren’t sufficiently secure, she may incorrectly reject systems that use 128-bit keys instead of 256-bit keys. In doing so, she may make choices that actually weaken her security overall. I might not agree with her reasoning, but we do have to recognize that her feelings do matter to her choices. And I certainly want to keep Molly secure. So if by offering 256-bit keys we enable Molly to make better security choices (even if for the wrong reasons), that is a good thing.

As long as there is no reason not to use 256-bit AES keys, it makes sense to use them. We have now reached the point where there is no harm in using 256-bit keys, and so the reassurance that comes with using them is worthwhile.

Now, security is a tough business. And tough people in a tough business can talk tough. When I threatened to shoot somebody if we used the expression “military grade” to describe our use of 256-bit AES keys, I wasn’t expecting that I’d have to shoot the guy who signs the checks. But a promise is a promise. So, Dave Teare, the gauntlet is down. Water pistols at dawn!

In conclusion

If there is any overall lesson here, beyond explaining why we’ve made the choices we have about key size for 1Password, it’s that seemingly simple questions about security and cryptography rarely have simple answers and explanations. On the one hand, we want people to understand what goes on under the hood and the thinking that goes into various design elements; but we also want to make it easy for people to behave securely without requiring that they understand what’s going on at the deeper levels.

Update: March 20, 2013

I reached out to the cryptographic community for any insight into Molly’s question about why the NSA insists that TOP SECRET material be encrypted using 256-bit keys. The answer came from Steven Bellovin of Columbia University:

@jpgoldberg @marshray Just heard that during the AES competition, NSA said in the open meetings it was for defense against quantum computing

Quantum computers, if they are every made practical, will be able to do amazing things. They will certainly change how we design cryptographic systems. It’s not that quantum computers will be faster or more powerful. Indeed, in some very important respects they will be less powerful than current computers. But there are some things that they will be able to do in less “time”. I put “time” in scare quotes because it has a different meaning in this context from the ordinary use of the word. Oh, what a big difference it is. In this context it means the number of distinct steps an algorithm must take in performing some computation.

Searching through “2 to the power of 128” keys (on a classical, non-quantum, computer) takes a number of steps that is proportional to “2 to the power of 128”. But for a quantum computer it takes a number of steps proportional to the square root of that number, “2 to the power of 64”. If a quantum computer is ever built capable of performing that task, we don’t know how the actual speed of each individual step will compare to those of current computers, but the NSA is taking no chances. Something with the effective strength of a 64-bit key isn’t strong enough. A 256-bit key against a quantum brute force attack would have the effective strength of a 128 bit key against a classical brute force attack.

I very much doubt that we will see a quantum computer actually capable of handing such things within the next thirty years. But if the past is any guide, my predictions about the future should be taken with a large grain of salt.

Jeffrey Goldberg

Principal Security Architect