
An otherwise excellent article over at The Inquirer has a very unfortunate title: AES encryption is cracked. AES is the Advanced Encryption Standard and is at the heart of so much encryption used today by governments, militaries, banks, and all of us. It is used by 1Password and less directly by Knox for Mac. It is the work horse of modern cryptography, and modern computer chips even have components built is to allow AES to be used efficiently. If AES were to be found weakened in any meaningful way, it would be very bad news for a lot of people.
Before I get into what has happened, I’d like to quote from the research paper itself: “As our attacks are of high computational complexity, they do not threaten the practical use of AES in any way.”
And quoting the Inquirer’s interview with Andrey Bogdanov, one of the researchers, we learn
“To put this into perspective: on a trillion machines, that each could test a billion keys per second, it would take more than two billion years to recover an AES-128 key,” the Leuven University researcher added. “Because of these huge complexities, the attack has no practical implications on the security of user data.” Andrey Bogdanov told The INQUIRER that a “practical” AES crack is still far off but added that the work uncovered more about the standard than was known before.
“Indeed, we are even not close to a practical break of AES at the moment.”
What’s the news
I’ve been trying to work through the actual paper and presentation slides by Andrey Bogdanov, Dmitry Khovratovich, and Christian Rechberger who were visiting Microsoft Research when they developed this. And although this research is far from having any practical influence on the use of AES it is actually fairly big news.
Cryptographers use the word “broken” in a very special way. If an attack on an algorithm can be computed with fewer computations than is required to check every single possible key, then the system is “broken”. Even if the improvement in the number of computations is negligible (as in this case) and even if other resources needed to get that small advantage are outrageously huge (again as in this case) it still gets called “broken”. But in this very specialized sense of the word “broken” the new research represents the first break of the full AES. It also displays the power of a technique developed earlier by the authors.
Impracticality #1: Impossible amounts of data
The authors calculate the best attack using their technique on AES with a 128 bit key requires storing 288 bits of data. That works out to about 38 trillion terabytes of data. Although estimates are hard to pin down, this is more than all the data stored on all the computers on the planet.
Impracticality #2: All for a two-bit gain
The number of encryptions that have to be performed to recover a 128 bit AES key is 2126.1 instead of the 2128 encryptions it would take to try all of the possible keys. This is a very small gain, as a 126-bit key (instead of 128-bits) would still take billions of years.
Impracticality #3: Lots of known plaintext needed
I may be misreading the research, but I believe that to discover an AES key, an attacker needs an enormous amount of known plaintext. That is, the attacker needs to already have a huge amount of information in both decrypted and encrypted form. I don’t know exactly how “huge” this will be, but I expect it to be far larger than any data anyone would or could encrypt using 1Password. I’m speculating here until I get a better grasp of things. Indeed, the amount is almost certainly related to the amount of data needed in “Impracticality #1”.
So this all doesn’t represent any threat to the practical use of AES for any purpose it is used for. An unfeasible amount of data needs to be stored in order to gain an insignificant improvement over just trying every key. But what it does do is highlight features of AES that make it subject to this kind of attack. Whether attacks based on this ever become any kind of real threat, we can bet that successors of AES will incorporate mechanisms to thwart them.
Where’s the meat? It’s in the middle
From here on out, I will try to explain some of what I understand from the new attack. There is much that I don’t understand of this, but I will give a broad outline and then wave my hands a bit. This part gets very technical, and I won’t be the slightest bit hurt if you stop reading here.
You may have heard of 3DES (Triple DES) which was used in many places before AES was settled upon as a replacement. The old Data Encryption Standard (DES) uses 56 bit keys. By the time we got into the 1980s it was absolutely clear that 56 bits was no longer enough for a key size. One could imagine (as many people did) taking two DES keys and just encrypting your data twice, first with one DES key and then taking that output and encrypting that with the second DES key. This, you might think, would get you the strength of a 112 bit key. It doesn’t.
It turns out that if you have an sample plaintext and ciphertext pair what you can do is try everyone one of the “2 to the power of 56” possible keys on the plaintext and also try everyone of the possible keys on the ciphertext as well. You will then find that there is an overlap of results. Some things that the plaintext encrypts into with one key will be the same as what the ciphertext decrypts into. This will give you (pretty much) the two 56 bit keys. This looking for where the output of one can meet up with the input of the other leads to this being called a “meet-in-the-middle” attack (not to be confused with a “man-in-the-middle” attack which is something else entirely). Note that in doing this, we “only” had to work through “2 to the power of 56” keys twice. That is the same as working through “2 to the power of 57” once. So double encrypting with DES only improved the security by one bit. This is why to get 112 bit strength out of DES we need to go through it three times, and so even though it allows for double the number of key bits, it is actually Triple DES.
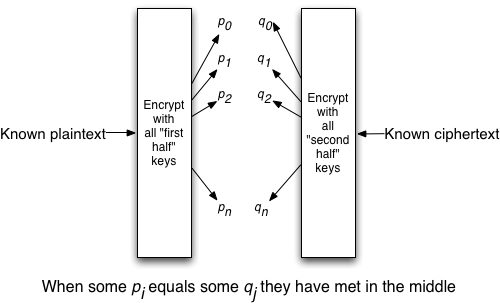
Now back to AES. Ciphers like AES go through multiple rounds of scrambling and manipulating the data. They also have various internal states as they process a block of data with a key. If we find an internal variable that allows us to break the encipherment into two halves then it is possible to do a meet-in-the-middle attack on that. AES, along with every modern cipher, is designed with this in mind. It is designed with enough rounds and interactions among them so that a standard meet-in-the-middle attack will not be quicker than simply trying every key.
Instead of doing the traditional meet-in-the-middle attack, the new attack constructs entities that group internal states, potential keys which complement each other in specific ways, and ciphertext into what they call “bicliques”. By using these more abstract entities instead of an intermediate variable, the attack can avoid some of the limitations on meet-in-the-middle attacks and be effective over a greater number of rounds. By carefully selecting which potential keys go into which biclique, some computation can be reduced by avoiding any duplication of effort. I still haven’t managed to understand, even in overview, how and why these bicliques do what they do, so I can’t say much more.
Thanks for joining me
If you’ve read this far (including the last section) then I thank you for joining me through my process of trying to understand this new attack on AES. Even though it has no practical implications, I find this stuff oddly fascinating. If you’ve just skipped right to the bottom (not an unreasonable thing to do at all) then let me say again everyone who has studied this, including the authors of the attack, state that this has no implications whatsoever for the practical use of AES.

 by Jeffrey Goldberg on
by Jeffrey Goldberg on

Tweet about this post